3754
A GPU-accelerated Extended Phase Graph Algorithm for differentiable optimization and learning1School of Information, The University of Texas at Austin, Austin, TX, United States, 2Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 3Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States, 4Diagnostic Medicine, Dell Medical School, The University of Texas at Austin, Austin, TX, United States, 5Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, United States
Synopsis
The Extended Phase Graph Algorithm is a powerful tool for MRI sequence simulation and quantitative fitting, but such simulators are mostly written to run on CPU only and (with some exception) are poorly parallelized. A parallelized simulator compatible with other learning-based frameworks would be a useful tool to optimize scan parameters. Thus, we created an open source, GPU-accelerated EPG simulator in PyTorch. Since the simulator is fully differentiable by means of automatic differentiation, it can be used to take derivatives with respect to sequence parameters, e.g. flip angles, as well as tissue parameters, e.g. T1 and T2.
Target Audience
MRI RF pulse and sequence developers and educators.Introduction
The Extended Phase Graph (EPG) Algorithm forms the backbone of many sequence simulations1,2 and is also used for quantitative fitting3,4. While developers increasingly share EPG simulators online in independent repositories, most are written to be run on CPU with minimal parallelization5. More recently, parallelized implementations have been developed6, though they are still limited to CPU and do not include auto-differentiation. Auto-Differentiation and GPU acceleration would enable the use of EPG within other physics-based learning frameworks7. Hence, an open source, parallelized and PyTorch8-based differentiable simulator could help develop and disseminate novel imaging techniques. This is similar to how packages like SigPy9, BART10, and MIRT11 have made advanced parallel imaging and compressed sensing reconstruction methods widely accessible. To satisfy this need, we developed a GPU-accelerated EPG implementation as part of the mri-sim-py Python package. Here, we describe the software’s goals, organization, and demonstrate a few examples of its usage.Software Design
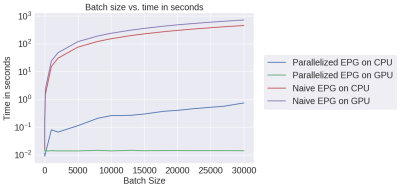
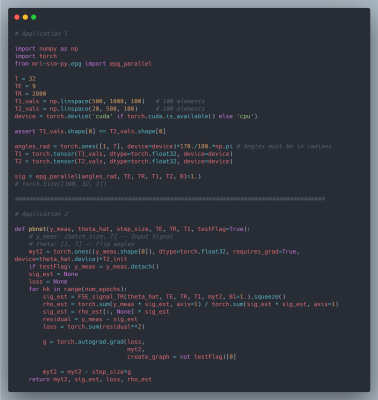
We chose mri-sim-py as the host package because it already contains different algorithms for simulating signals and this was a natural extension. Python was chosen as it can be demonstrated easily by means of Jupyter notebooks and interfaced with PyTorch, a popular machine learning auto-differentiation framework. The EPG Algorithm has three components: RF excitation, gradient application, and tissue relaxation. Figure 1a shows how these three components of the EPG algorithm are organized. Figure 1b shows 100 signals simulated using various values of T1 and T2 for a multi-echo spin-echo sequence with 60-degree refocusing flip angles. Figure 2 shows a comparison of the time taken by the naive and our parallelized EPG simulators running on CPU and GPU respectively. We can see that the increase in batch size has negligible impact on the evaluation time of the parallelized EPG algorithm running on GPU. Figure 3 shows code snippets for two applications. Application 1 shows how to use the algorithm to generate signal values from a fast spin-echo simulation using the flip angle train, T1 and T2, TE, TR, and B1 parameters. Application 2 shows how to use auto-differentiation to estimate T2 relaxation, as described below in detailApplication Examples
We show an application to estimating T2 relaxation. A volunteer was scanned under IRB approval and informed consent. A multi-echo spin-echo acquisition of the brain was acquired on a 3 Tesla Siemens Vida scanner. Scan parameters included: 32 echoes, TR=2800 ms, TE=9 ms, matrix size=288x288, nominal refocusing flip angles of 105 degrees. Using the EPG simulator, a least-squares solver with gradient descent was implemented (Figure 3, Application 2), taking advantage of automatic differentiation. Figure 4a and 4b show images of the resulting Proton Density map and T2 map respectively, which was estimated in 543 seconds using batch size = 14,000, for a total number of 58 million signal evaluations. We also show how the result of optimizing the flip angles of a multi-echo spin-echo experiment using the Cramer Rao lower bound12. The optimized flip angle train is shown in Figure 4c. A third application, shown in Figure 5, combines the simulator with a fully connected neural network for estimating T1 and T2, where again the flip angle train is optimized via auto-differentiation to minimize fitting error.Availability
The latest version of this tool is available from the Github repository of mri-sim-py at https://github.com/utcsilab/mri-sim-py/tree/master/epg. Installation instructions are provided in the README file present there. Jupyter notebooks containing examples are also available at the same repository inside epg_parallel folder.Acknowledgements
This work was supported by the Amazon AWS Machine Learning Research grant.References
1. Hennig, Jürgen. "Multiecho imaging sequences with low refocusing flip angles." Journal of Magnetic Resonance (1988) 78.3 (1988): 397-407.
2. Weigel, Matthias. "Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple." Journal of Magnetic Resonance Imaging 41.2 (2015): 266-295.
3. Ben‐Eliezer, Noam, Daniel K. Sodickson, and Kai Tobias Block. "Rapid and accurate T2 mapping from multi–spin‐echo data using Bloch‐simulation‐based reconstruction." Magnetic resonance in medicine 73.2 (2015): 809-817.
4. McPhee, Kelly C., and Alan H. Wilman. "Transverse relaxation and flip angle mapping: evaluation of simultaneous and independent methods using multiple spin echoes." Magnetic resonance in medicine 77.5 (2017): 2057-2065.
5. Hargreaves, Brian A., “Extended phase graph Matlab algorithm.” (2012) Available at https://web.stanford.edu/~bah/software/epg/. Downloaded Dec 2020.
6. Lamy, Julien, and P. Loureiro de Sousa, “Sycomore: an MRI simulation toolkit.” Proceedings of the ISMRM 28th Annual Meeting, Online. Vol. 4819. 2020.
7. Kellman, Michael R., et al. "Physics-based learned design: Optimized coded-illumination for quantitative phase imaging." IEEE Transactions on Computational Imaging 5.3 (2019): 344-353.
8. Paszke, Adam, et al. "Pytorch: An imperative style, high-performance deep learning library." Advances in neural information processing systems. 2019.
9. Ong, F., and M. Lustig. "SigPy: a python package for high performance iterative reconstruction." Proceedings of the ISMRM 27th Annual Meeting, Montreal, Quebec, Canada. Vol. 4819. 2019.
10. Martin, U., et al. "Berkeley Advanced Reconstruction Toolbox (BART)." Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Canada. 2015.
11. Fessler, J. A. "Michigan image reconstruction toolbox." (2018), available at https://web.eecs.umich.edu/~fessler/code/. Downloaded Dec 2020.
12. Tamir, Jonathan I., et al. "Computational MRI With Physics-Based Constraints: Application to Multicontrast and Quantitative Imaging." IEEE Signal Processing Magazine 37.1 (2020): 94-104.
Figures